GAN : Vers une meilleure estimation des distributions ?

Les Réseaux Antagonistes Génératifs (GAN) sont un nouveau type de réseau de neurones profonds (deeplearning).
Leur objectif est de pouvoir estimer et représenter une distribution de données.

Ce type de réseau a été introduit par Ian Goodfellow en 2014 [1].
Il présente un framework composé de deux modèles : un générateur et un discriminateur.
Le générateur (que nous appellerons G) a pour objectif de produire des données artificielles semblables aux données réelles.
Le discriminateur (que nous appellerons D) a pour objectif de différencier les données générées par le générateur G des données d’apprentissage.

Les GANs sont des réseaux utilisant un apprentissage non supervisé. C’est-à-dire que l’apprentissage du réseau se fait sans étiquette. De ce fait, leur apprentissage nécessite uniquement un dataset contenant les données dont nous voulons apprendre la distribution.

Définition des GANs

Ce framework s’inspire des études sur la théorie des jeux. Dans les GANs, il y a deux modèles antagonistes. Le générateur G cherche à tromper le disciminateur D en générant des données similaires aux données réelles (dataset d’apprentissage). L’apprentissage d’un GAN peut être assimilé aux interactions entre un faussaire et un policier.
Le faussaire cherche à produire des oeuvres ou des billets semblables aux faux, tandis que le policier cherche à identifier les faux du vrai. Dans cet exemple, la qualité de production du faussaire dépend du policier, car plus le policier est bon, plus le faussaire doit améliorer ses faux. Il en est de même pour le policier, puisque sa capacité de détection dépendra de la qualité des faux.
Plus les faux seront de bonne qualité, plus il devra trouver de nouvelles caractéristiques permettant de distinguer le faux du vrai.

À partir de cette analogie, on peut dériver la stratégie d’apprentissage d’un GAN. On peut définir la fonction comme étant la fonction représentant le discriminateur. Cette fonction prend en entrée une donnée et retourne une valeur entre et . Si le discriminateur juge que la donnée est fausse, sera proche de . Dans le cas contraire, le discriminateur renverra une valeur proche de .

On peut également définir la fonction comme étant la fonction représentant le générateur. Cette fonction prend en entrée un vecteur de bruit ou autre (voir variantes de GAN présentée ci-dessous) et renverra une donnée de la même dimension que .

Goodfellow a défini la fonction de coût des GANs tel que:

(1)  

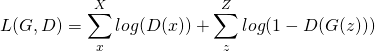
Tel que X est le set de données réelles et Z est l’ensemble de vecteurs de bruit.
La fonction se base sur la formule de Jensen-Shannon et mesure la divergence entre deux distributions.

Cette formulation reflète bien la logique derrière les GANs, mais elle a un défaut. La formule originale utilise la fonction , mais celle-ci n’est pas définie en . Donc la fonction de coût ne pourra pas être définie dans certains cas extrêmes, par exemple si le discriminateur renvoie pour une vraie donnée ou s’il renvoie pour une fausse donnée. Ce problème peut être résolu en ajoutant des constantes afin d’éviter de calculer des .

Par ailleurs, dans l’article [2], les auteurs ont montré que la formulation originale comporte un autre défaut. Selon eux, la mesure utilisée n’est pas assez sensible. Dans leur article, ils ont comparé plusieurs méthodes évaluant la distance entre deux distributions, dont la distance de Wasserstein.

À partir de cette mesure, ils proposent la fonction de coût suivante:

(2)  

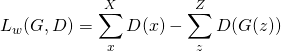
Cette nouvelle formulation semble simple, mais elle implique une contrainte forte. L’utilisation de cette formule pour l’apprentissage d’un GAN nécessite que le générateur soit une fonction de Lipschitz localement. Les auteurs suggèrent dans leur article de « clipper » les poids du générateur.

Le problème est que la constante permettant le « clippage » est dépendante de l’architecture du générateur, ainsi que des données. Cette méthode, bien qu’artisanale, est utilisée dans un premier temps, puis remplacée par l’approche proposée dans [3]. Les auteurs proposent de pénaliser la fonction d’apprentissage plutôt que de clipper les poids du générateur. Pour cela, ils introduisent un nouveau terme dépendant de la dérivée de la fonction de coût de Wasserstein.
La fonction devient donc:

(3)  

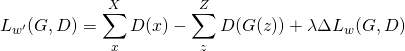
Cette nouvelle formulation permet de garantir la contrainte de Lipschitz, mais introduit un nouvel hyperparamètre à notre méthode. Malgré le fait que les deux méthodes possèdent le même nombre d’hyperparamètres, la version améliorée reste plus facile à optimiser.

Cas d’usage dans la littérature

Depuis la parution de l’article de Goodfellow, de nombreux articles autour des GANs ont été publiés. De nombreux cas d’usage et d’architectures ont été proposés.

Les articles concernant les GANs se concentrent énormément autour de la génération d’image, de vidéo ou de son. À l’origine, la majorité des travaux se concentrait sur la génération d’images aléatoires, puis la génération d’images sous contraintes. La maitrise des GANs a énormément évolué entre la première formulation de la méthode et les méthodes utilisées actuellement. Au début, les méthodes produisaient des images de visages qui semblaient humains. Les visages générés ressemblaient à des visages humains, mais les proportions n’étaient pas bien conservées. Actuellement, on arrive à générer des visages qui sont presque indiscernables.

En terme de méthode, on peut distinguer deux types de GANs : ceux utilisant uniquement un vecteur de bruit, comme input pour le générateur et ceux utilisant un vecteur de bruit ainsi que des données additionnelles.

On peut distinguer deux types de GANs (voir Figure 1).

Les GANs du premier type sont similaires au framework présenté ci-dessus, même si leur architecture peut être différente. Les GANs du deuxième type sont appelés des GANs conditionnels. Ces GANs sont, selon moi, les plus intéressants, car ils permettent de générer de la data en fonction de conditions. Dans le cadre de cet article, nous allons nous concentrer sur les GANs du second type. Selon nous, ces algorithmes semblent les plus prometteurs, même si les premiers algorithmes sont importants et intéressants.

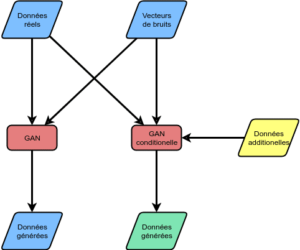
Figure 1 – Différence entre les GAN et les GANs conditionnels.

La volonté derrière les GANs du second type est de pouvoir contrôler la génération des données. Car, dans la première version du framework, il n’était pas possible de spécifier la génération. Par exemple, les premiers modèles générant des photos de visages étaient purement aléatoires. Mais, avec les approches du second type, les algorithmes peuvent générer des visages souriants, fâchés, âgés ou jeunes. Une partie de ces algorithmes a été utilisée pour générer les deepfakes que nous connaissons à l’heure actuelle.

L’un des premiers formalismes des GANs du second type a été présenté dans l’article [4]. Dans cet article, les auteurs avaient pour objectif d’inclure des données additionnelles telles que les étiquettes. Par exemple, dans le cas du dataset MNIST (dataset de chiffres manuscrits), les auteurs ont utilisé les étiquettes des données d’entrée afin de pouvoir contrôler la génération. Avec un GAN entrainé ainsi, il est possible de spécifier le chiffre que nous voulons générer.

Cela est possible en modifiant les fonctions de générateur et de discriminateur. Dans le framework original, la fonction du générateur et la fonction du discriminateur utilisent respectivement un vecteur de bruit et un vecteur représentant une donnée. Dans le framework proposé dans l’article [5], les auteurs proposent d’étendre les données d’entrée de ces fonctions. Pour cela, les auteurs redéfinissent ces fonctions, telle que la fonction du générateur devient et la fonction du discriminateur . La variable représente les données additionnelles. Avec cette formulation, les GAN peuvent apprendre à générer des données en fonction de mais aussi à identifier le vrai du faux en fonction de .

Ce nouveau framework a permis la création de réseaux très intéressants. Par exemple, dans l’article [5], les auteurs ont défini un GAN permettant de retirer le bruit d’une image (voir Figure 2). Ou encore les travaux de NVIDIA comme par exemple le ArchiGAN ou encore leur édition de photo utilisant des GANs.

Figure 2 – Exemple d’un GAN éliminant le bruit d’une image (source [5]).

Cas d’étude chez Aquila

Chez Aquila, nous nous sommes penchés sur une utilisation des GANs peu courante. Nous avons voulu générer des séries temporelles sous contraintes. La notion de contraintes est importante pour nous, car dans nos différents cas d’usages, les séries temporelles sont intimement liées à des variables externes.

Dans notre cas d’étude, nous nous sommes concentrés sur la consommation électrique. Intuitivement, nous savons que la consommation électrique dépend de la température extérieure (chauffage, climatisation, etc.) mais aussi de la date (période de vacances, périodes d’activité, etc.). Pour le développement de notre approche, nous avions à disposition des informations liées à la date et la série temporelle de consommation sur 5 ans. Le modèle a été ensuite évalué sur une dernière année qui n’a pas été utilisé durant l’apprentissage.

Notre objectif avec ce modèle était de pouvoir prédire l’évolution de la consommation à J+1 en générant la suite de notre série temporelle. Pour cela, nous utilisons les évolutions de consommations sur la dernière semaine, plus les informations calendaires disponibles. Le modèle a été évalué contre un modèle simple où nous prenions la valeur J-7 pour prédire J+1 et un random forest. Le modèle basique nous a servi de base afin d’améliorer le random forest et notre GAN.

Nous avons évalué les modèles en calculant le biais entre les vraies valeurs et les valeurs générées:

(4)  

Notre baseline affichait un biais d’environ sur l’année, tandis que le random forest affichait un biais d’environ .
Notre modèle utilisant les GANs affichait un biais d’environ . Le constat le plus intéressant avec notre modèle utilisant les GANs est qu’il a réussi à apprendre les spécificités du mois de mai. Sur le mois de mai, la consommation électrique montre une fluctuation plus grande à cause des jours fériés. Les modèles essayés montrent quelques difficultés sur ce mois, car la consommation a un lien plus fort avec les données calendaires. Le modèle utilisant des GANs a montré qu’il était capable d’identifier comment utiliser au maximum l’information de nos contraintes, afin de coller à la distribution des données.

Pour conclure, nous avons montré comment ont évolué les GANs depuis la première définition par Goodfellow. Les premiers algorithmes faisaient des générations aléatoires, tandis que les nouvelles versions deviennent plus précises et contrôlables. Par ailleurs, il faut noter que les domaines d’utilisation des GANs évoluent fortement. La preuve est que dans notre cas d’étude, nous avons pu générer des séries temporelles précises, même dans les périodes compliquées comme le mois de mai.