Interprétabilité des modèles de Machine Learning

Interprétabilité

Retrouvez toutes nos autres videos sur notre chaîne YouTube. 

 

Comprendre les modèles : un enjeu fondamental

Les modèles de machine learning (ML) sont souvent des boites (plus ou moins) noires qu’on évalue selon leurs performances sur un ensemble de données, sans savoir exactement pourquoi et comment les décisions sont prises. Or, si obtenir les meilleures performances possible peut suffire dans certains cas, on s’aperçoit que comprendre les décisions est de plus en plus indispensable. Un exemple : un modèle de ML préconise de refuser d’accorder un prêt à un individu. Si cet individu demande des explications, son conseiller doit pouvoir les lui fournir.

On distingue plus précisément deux grandes catégories d’avantages à pouvoir interpréter un modèle.

Du côté Data Scientist :

• Déterminer quand et pourquoi le modèle se trompe
• Valider la cohérence du modèle
• Donner confiance au métier vis-à-vis du modèle choisi

Du côté métier :

• Pouvoir justifier les décisions (auprès d’un client par exemple)
• Gagner en transparence
• Être en adéquation avec la réglementation (aspect légal, audit, etc)

Plusieurs solutions existent pour mieux comprendre les décisions. Il est possible d’utiliser des modèles directement interprétables (régression linéaire ou logistique, arbre de décision…), mais ce sont des modèles plus simples qui donnent généralement de moins bons résultats. L’autre approche est d’extraire des informations du modèle afin de comprendre ses prédictions, soit globalement pour expliquer sur quoi se base le modèle pour prédire, soit localement pour expliquer chaque décision.

Dans la suite, nous nous sommes en particulier intéressé à l’extraction d’informations (locales ou globales) de modèles utilisés sur des données tabulaires, c’est-à-dire de données représentées par plusieurs variables, avec :

• Une ligne par donnée
• Une colonne par variable

Pour ces données, il est possible de calculer l’importance de chaque variable pour le modèle. A noter que :

• Il faut utiliser un modèle déjà entraîné
• Plusieurs calculs d’importances sont possibles
• Certaines méthodes sont utilisables quel que soit le modèle, même un modèle de type black box, inconnu ou de type deep-learning.

La suite de cet article s’intéresse aux différents calculs d’importance de variables (features importance), en particulier pour les modèles de forêt aléatoire (random forest) et xgboost, pour lesquels les librairies Python sklearn et xgboost (respectivement) proposent de base plusieurs calculs. Nous allons cependant montrer leurs limites, et pourquoi il vaut mieux utiliser la permutation importance ou SHAP. Nous montrerons ensuite différents graphiques de la librairie SHAP permettant d’analyser les prédictions d’un modèle.

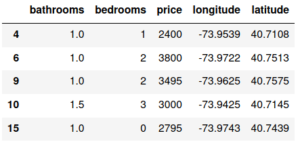
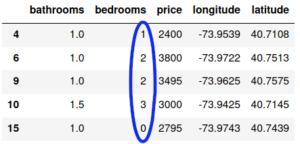
Les données utilisées pour l’exemple sont celle du Kaggle « Two Sigma Connect: Rental Listing Inquiries ». Le but est de prédire la popularité (« interest_level ») d’un appartement selon ses caractéristiques (certaines informations disponibles dans le jeu de données Kaggle n’ont pas été utilisées ici). Les appartements sont situés à New York. Un échantillon des données donne :

Une rapide exploration des données nous montre qu’il s’agit d’un problème avec des classes déséquilibrées (la classe 1, « low », est majoritaire) :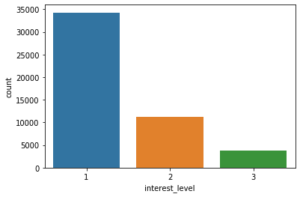

Le code utilisé pour générer les images de cet article est disponible en ligne : https://github.com/aureliale/features_importance. Deux notebooks y sont disponibles, dont cet article reprend le déroulé.

1. Exploration des feature importances

 

1.1 Feature importances de la librairie xgboost

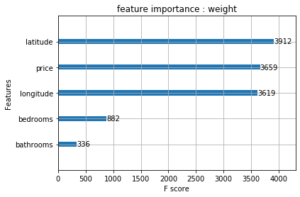
La librairie xgboost propose directement trois types de features importance. Après entraînement d’un modèle XGBoost, voici les graphiques représentants ces importances :

a/ Feature importance : weight

Il s’agit du nombre de fois où une variable est utilisée pour diviser les données à travers l’ensemble des arbres.

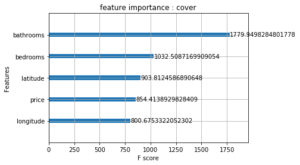
b/ Feature importance : cover

Il s’agit du nombre de fois où une variable est utilisée pour diviser les données à travers l’ensemble des arbres, pondéré par le nombre de données (d’entraînement) passées par ce noeud. On peut en effet avoir des noeuds créés lors de l’entraînement, mais où presque aucune donnée ne circule : on considère donc que l’influence de ce noeud est moindre.

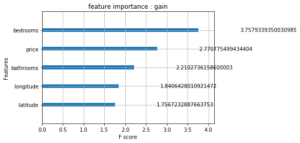
c/ Feature importance : gain

Il s’agit de la moyenne de la réduction de la fonction coût (pour les données d’entraînement) quand une variable est utilisée pour une division au niveau d’un noeud.

ANALYSE

Les trois importances… donnent des résultats complètement différents ! Selon quels critères choisir le calcul d’importance ? Qui plus est, même si l’importance « gain » peut paraître plus pertinente en théorie, elle reste une information tirée des données d’entraînement : comment savoir si elle se généralisera aux données de test ?

 

1.2 Feature importances de RandomForest (sklearn)

a/ Mean decrease in impurity

Sklearn est une librairie très utilisée en machine learning, et propose en particulier une implémentation de forêt aléatoire avec une feature importance intégrée au modèle, appelée mean decrease in impurity (MDI), aussi appelée Gini importance. Dans sklearn, il s’agit de calculer la réduction de l’impureté des noeuds (pondérée par la proportion de données d’entraînement passant par ce noeud) moyennée sur tous les arbres de l’ensemble. Ce calcul se rapproche de la « gain importance » de xgboost.

Pour un modèle de forêt aléatoire (entraîné), on obtient le graphique :

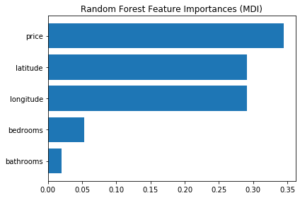
On peut être tenté de le comparer aux graphiques précédents (en particulier gain importance de xgboost) mais il faut garder à l’esprit que ce sont différents modèles, qui peuvent prendre des décisions de manières différentes. Il est cependant étonnant que les nombres de chambres et de salles de bains paraissent si peu importants dans la prise de décision.

b/ Permutation importance

Depuis l’été 2019, sklearn propose également le calcul de la permutation importance.

Pour un jeu de donnée, pour une variable i, on regarde la différence de performance entre :

• les données telles quelles
• les données où on permute entre elles les valeurs de la variable i

Par exemple, pour calculer l’importance de la variable bedrooms, on va mélanger toutes les valeurs de la colonne bedrooms entre elles.

L’idée vient du fait qu’on souhaiterait comparer les performances du modèle en utilisant/sans utiliser la variable en question. Bien que faisable, cette technique est très coûteuse : il faudrait entraîner un nouveau modèle pour chaque variable supprimée. On peut simuler cette suppression en mélangeant les valeurs d’une variable, afin qu’elle n’apporte plus aucune information au modèle. Étant donné l’aspect aléatoire, il est bien de répéter plusieurs fois le calcul afin d’avoir une meilleure approximation.

Le graphique pour les données d’entraînement donne :

L’énorme avantage de cette méthode est qu’il est possible de l’utiliser également sur des données de test (et éventuellement de choisir le score utilisé pour évaluer les changements de performance) :

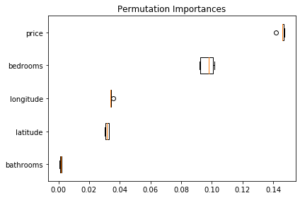
On remarque en particulier que les informations latitude/longitude paraissent beaucoup plus importantes sur les données d’entraînement que de test : elles entraînent sûrement du sur-apprentissage ! Cela illustre la nécessité de calculer l’importance des variables sur des données de test et non sur les données d’entraînement.

 

1.3 Ajout d’une variable aléatoire

Afin de se convaincre de la pertinence ou pas de certains calculs d’importance, il est possible d’ajouter aux données une variable aléatoire continue, entre 0 et 1, qui ne devrait donc pas avoir d’incidence sur les résultats du modèle.

Voici les résultats pour la mean decrease in impurity :

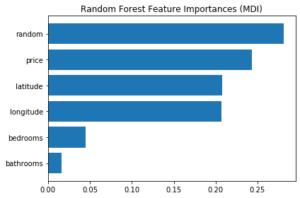
Étonnement… la variable aléatoire paraît être la plus importante dans la prise de décision du modèle ! Cela est dû au fait que :

– c’est une variable continue, qui est utilisée plus facilement plus souvent pour effectuer des séparations dans les noeuds des arbres

– l’importance MDI dépend des données d’entraînement et non de test

Si on calcule la permutation importance pour les données d’entraînement, on obtient :

Et pour les données de test :

On s’aperçoit que la variable aléatoire n’a effectivement aucun effet sur les performances pour l’ensemble de test. Par contre, pour les données d’entraînement, elle paraît être utilisée de manière non négligeable… sans doute à cause d’un modèle trop expressif.

SHAP est une autre technique qui sera davantage détaillée plus tard. Les graphiques suivants sont semblables à ceux de la permutation importance (pour les données d’entraînement puis de test) :

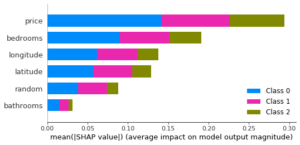
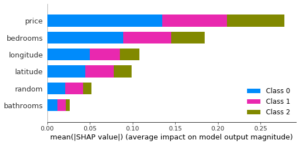
L’avantage de SHAP est que la technique vérifie des propriétés précises, et qu’il est possible d’obtenir des informations par rapport à chaque donnée (et donc comme illustré ici, pour chaque classe). L’avantage de la permutation importance est qu’il est possible d’utiliser une métrique au choix, et que des valeurs d’importances très faibles préviennent de variables inutiles OU de variables très corrélées comme nous le verrons juste après.

 

1.4 Corrélations entre variables

a/ Duplication d’une variable

Les corrélations entre les variables peuvent fausser l’interprétation des importances. Pour simuler la corrélation entre deux variables, il est possible d’en dupliquer une à l’identique. On va par exemple dédoubler la variable bedrooms en bedrooms_bis.

Dans ce cas, toujours pour un modèle de forêt aléatoire, sur l’ensemble de test, on obtient :

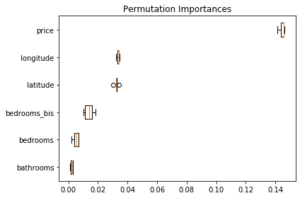
Pour rappel, le même graphique sans dédoubler la variable bedrooms donne :

Ainsi, un modèle appris sur des données avec deux variables bedrooms  et bedrooms_bis (identiques) donne l’impression que cette variable n’est pas importante ; alors qu’elle paraît l’être lorsqu’elle n’apparaît qu’une fois dans les données ! Les importances sont en effet partagées entre les variables corrélées : le modèle peut utiliser les informations de la variable bedrooms_bis s’il n’utilise pas celles de la variable bedrooms. Selon le modèle et la méthode de calcul de l’importance des variables, les effets seront plus ou moins marqués, mais il faut garder à l’esprit que les calculs d’importance de variables ne font jamais bon ménage avec les corrélations entre variables. SHAP donne des résultats semblables (toujours sur l’ensemble de test) :

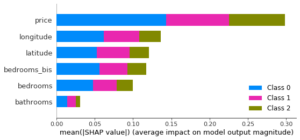
b/ Permutation jointe de plusieurs colonnes

Dans le cas de la permutation importance, il est possible de permuter en même temps plusieurs colonnes. C’est-à-dire que si on permute en même temps les variables bedrooms et bedrooms_bis, les valeurs de ces deux variables de la donnée n°1 vont par exemple se retrouver toutes les deux pour la donnée n°2. Ainsi, si l’on sait que deux variables sont corrélées, on peut tester l’importance jointe de ces variables. La librairie rfpimp, dédiée à la permutation importance, permet ce calcul.

Par exemple, pour la forêt aléatoire, sur l’ensemble de test :

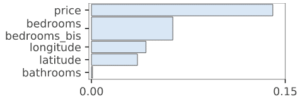
alors que la permutation importance de base donne :

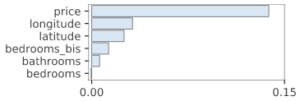
Permuter en même temps des variables corrélées peut donc permettre d’avoir une meilleure idée de leurs effets sur les résultats du modèle.

Ainsi, pour un modèle avec de bons résultats, quand l’importance d’une variable est faible cela signifie :

– soit que le modèle n’utilise pas beaucoup cette variable

– soit que la variable est très corrélée à une ou plusieurs autres variables et qu’on ne distingue donc pas sa réelle importance

1.5 Utilisation d’une autre métrique

L’avantage de la permutation importance est qu’elle se calcule par rapport à une métrique (choisie) : il est donc possible d’adapter cette métrique au problème. Par exemple, dans ce cas, il est possible d’utiliser la balanced accuracy, plus informative pour des classes déséquilibrées. Les différences ici ne sont cependant pas très importantes, comme on peut le voir sur l’ensemble de test avec la balanced accuracy :

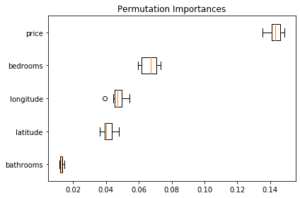
alors que l’accuracy habituelle donnait :

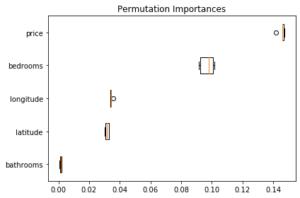
2. SHAP (Shapley Additive exPlanations)

La permutation importance présente deux inconvénients majeurs : elle se calcule sur un ensemble de données et non sur une donnée unique, et il est nécessaire de connaître la vraie sortie pour calculer la mesure d’évaluation.

L’utilisation des valeurs SHAP permet de palier à ces inconvénients. Cette technique a été présentée par Scott M. Lundberg en 2017 ; elle permet d’expliquer localement la sortie de n’importe quel modèle de machine learning.

Pour la prédiction d’un modèle, SHAP calcule les contributions de chaque variable à cette prédiction ; l’explication est exprimée comme une fonction linéaire des M variables :

avec φ₀ la valeur de base du modèle,
et z_i=1 si la variable i est présente, 0 sinon.

Cette technique est basée sur les valeurs de Shapley (venant de la théorie des jeux) : pour toutes les combinaisons de variables autres que i, on évalue la différence sur la sortie f(x) entre si on utilise cette variable ou pas. Les explications complètes sont disponibles dans les articles scientifiques dédiés, ou dans un autre article sur le blog d’Aquila : https://www.aquiladata.fr/shap-mieux-comprendre-linterpretation-de-modeles/.

Pour résumer, la méthode SHAP a été conçue comme vérifiant trois propriétés jugées nécessaires afin d’expliquer correctement un modèle :

• Missingness : les variables manquantes n’ont aucun impact
• Consistency : changer le modèle de telle manière qu’une variable a un plus fort impact ne réduira jamais la valeur de contribution de cette variable (permet de comparer les feature importances de différents modèles)
• Local accuracy : la somme des valeurs de contribution des variables est égale à la sortie du modèle

Comme le calcul exact des valeurs de Shapley est difficile, le calcul se fait de manière combinée avec d’autres méthodes d’explication de modèles. La librairie shap en python implémente plusieurs de ces techniques, en particulier :

• Tree Explainer (version exacte et rapide pour les arbres de décision)
• Deep Explainer (approximation rapide pour les Deep Neural Networks)
• Gradient Explainer (autre méthode utilisant SHAP pour les Deep NN)
• Kernel Explainer (approximation pour n’importe quel modèle)

Dans la suite, nous allons montrer des exemples d’utilisation du Tree Explainer pour expliquer les résultats d’une forêt aléatoire. La librairie propose en effet de nombreux graphiques afin d’explorer les résultats du modèle.

Les données et les modèles utilisés sont les mêmes que précédemment.

 

2.1 Summary_plot : graphiques généraux

SHAP permet de calculer, pour chaque donnée, l’importance de chaque variable. Il suffit de faire la moyenne des importances afin d’avoir des importances « globales » pour chaque variable, comme les méthodes précédentes permettaient de le faire.

On obtient les graphiques suivants, sur les données d’entraînement puis de test :

 

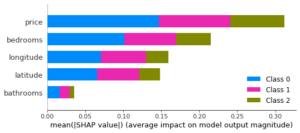
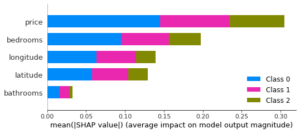
Cependant, l’énorme avantage de SHAP est que la technique permet d’avoir une information plus précise pour chaque donnée. Il est ainsi possible de dessiner ce type de graphique :

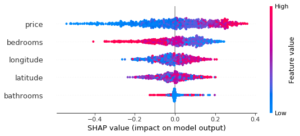
Ici, chaque point correspond à une donnée (de test). Les valeurs SHAP (abscisse) sont représentées pour chaque variable (ordonnée), pour chaque donnée. La couleur représente la valeur de la variable. Des « épaisseurs » plus importantes sur l’axe des ordonnées (par exemple pour la variable bathrooms en abscisse 0) permettent de représenter une densité de points plus importante.

Sur ce graphique qui correspond à la classe 0 (« low interest »), on comprend donc qu’un prix élevée rend l’appartement moins intéressant (car une valeur SHAP élevée, donc une appartenance plus forte à la classe 0), alors qu’un nombre de chambres faible rend l’appartement moins intéressant. Les résultats sont plus difficiles à interpréter pour la latitude, ce qui peut être normal car son influence peut être fortement liée à la valeur de longitude.

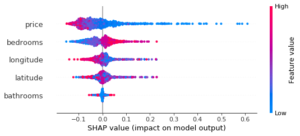
Ces graphiques peuvent être dessinés pour chaque classe, par exemple pour la classe 2 « high interest » on obtient un graphique presque inverse :

 

2.2 Force_plot : graphique pour une donnée

Ces informations sont également affichable pour UNE donnée avec le force_plot. Par exemple pour une donnée de la classe 0 « low » (correctement prédite), on obtient :

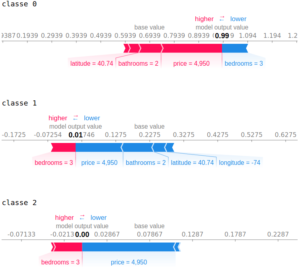
La valeur de base (base value) est la valeur moyenne obtenue comme sortie pour cette classe, alors que la valeur de sortie (model output value) est la valeur prédite par le modèle. Les valeurs SHAP de chaque variable, proportionnelles aux tailles des flèches, « poussent » la prédiction depuis la valeur de base jusqu’à la valeur prédite. Ainsi, dans le cas de cette donnée, les valeurs des variables bathrooms et price sont déterminantes pour dire que la donnée appartient à la classe 0, alors que c’est surtout la valeur de price qui permet de dire que la donnée n’appartient pas aux classes 1 et 2.

A noter que dans le cas où il n’y a que deux classes, un seul graphique suffit à avoir l’information nécessaire.

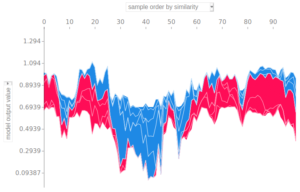
Les informations de plusieurs données sont affichables sur un même graphique en tournant de 90° les graphiques précédents :

 

2.3 Decision_plot : montre comment un modèle arrive à la décision

Le decision_plot permet d’afficher les mêmes informations que le force_plot sous un autre format. Par exemple, pour la même donnée que précédemment, pour la classe 0, on obtient :

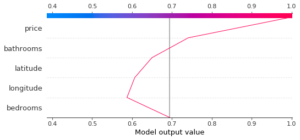
L’avantage de ce graphique est qu’il est possible d’afficher plusieurs courbes en même temps. Par exemple, dans le cas multi-classes, il est possible d’afficher les  valeurs SHAP pour les différentes classes avec le multioutput_decision_plot :

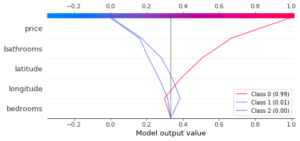
La model output value est cette fois la valeur moyenne des output values pour les différentes classes, et les valeurs SHAP sont décalées afin de correctement reproduire le score de sortie du modèle. On peut ainsi facilement comparer les effets des variables sur les prédictions des différentes classes.

Il est également possible de comparer les importances des variables pour plusieurs données. Pour une même classe (ici la classe 0 « low interest »), pour plusieurs données, on obtient :

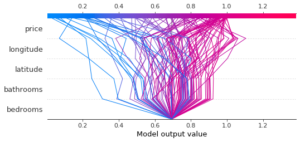
Le graphique n’est pas forcément très utilisable tel quel, mais il est possible de n’afficher qu’un sous-ensemble des données, par exemple celles pour lesquelles le modèle prédit la classe 2 « high interest » :

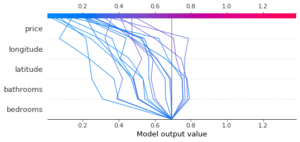
Ainsi, ce graphique est un outil supplémentaire pour explorer les résultats du modèle, et comprendre par exemple pourquoi certains exemples sont mal classés, ou détecter des outliers.

 

2.4 Dependence_plot : effet des variables les unes sur les autres

Le dependence_plot permet, comme son nom l’indique, d’explorer les dépendances entre variables.

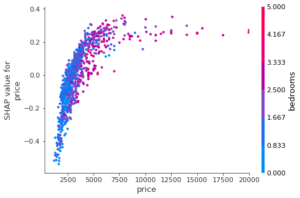
Chaque point correspond à une donnée ; son abscisse correspond à la valeur de la variable choisie (price ici) et son ordonnée à la valeur SHAP de la variable. On voit ici que les prix faibles, à gauche, ont une valeur SHAP négative (les données appartiennent moins à la classe 0 « low interest ») alors que les prix élevés, à droite, ont des valeurs SHAP plus importantes et donc poussent davantage la prédiction vers la classe 0.

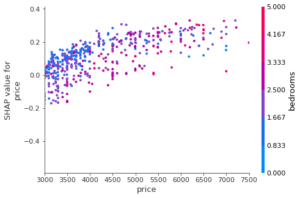
Si on zoom sur une valeur de prix, par exemple vers les 4000 ou 5000, on remarque l’influence de la variable bedrooms qui correspond aux couleurs des points : pour un même prix, les points rouges (plus de chambres) sont plus bas que les points bleus (moins de chambres) : une valeur de prix élevée, associée à peu de chambres, pousse davantage la donnée vers la classe 0 que une donnée avec le même prix mais avec plus de chambres.

Si on explore les variables latitude et longitude, on obtient :

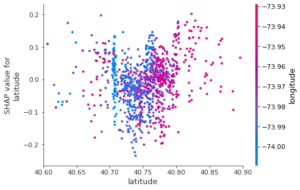
qui est beaucoup moins informatif, et pour cause : le modèle utilise beaucoup moins ces variables, et il faudrait sans doute retravailler la géolocalisation pour en tirer davantage d’information pour ce modèle.

 

2.5 Conclusion sur SHAP

Les valeurs SHAP sont utilisables comme les autres importances de variable afin de savoir, globalement, quelles variables sont les plus influentes sur les prédictions d’un modèle. Elles permettent cependant une exploration beaucoup plus poussée des prédictions, et peuvent par exemple permettre de comprendre pourquoi certaines données sont mal classées (en affichant les graphiques spécifiques à ces données et en les comparant à d’autres données semblables). L’analyse de ces graphes peut aller de paire avec l’analyse de données, cette fois pour comprendre la modélisation.

Cette étude doit cependant être faite sur un modèle avec des résultats convenables, car les valeurs SHAP risquent de ne pas avoir de sens si elles sont calculées sur un modèle qui renvoie de mauvais résultats et qui n’a pas appris à tirer les bonnes informations des variables.

Conclusion

Pour conclure sur l’importance des variables :

• Il ne faut pas utiliser les features importances « de base », mais utiliser la permutation importance ou SHAP
• La permutation importance :
  • donne des explications globales, sur un ensemble de données
  • permet de différencier entre les données d’entraînement et de test
  • permet de choisir la mesure d’évaluation
  • nécessite de connaître la vraie sortie pour évaluer l’importance des variables (car calcul de la mesure d’évaluation)
  • alerte sur les variables peu utilisées ou très corrélées lorsque les valeurs d’importances sont très faibles (ce qui n’est pas autant visible avec SHAP)
• SHAP :
  • donne des explications locales, pour UNE donnée
  • est utilisable pour expliquer les prédictions de nouvelles données, même si on ne connaît pas la vraie sortie
  • étudie également l’interaction entre les variables
• Les importances de variable renseignent comment ce modèle, tel qu’il est entraîné, utilise les variables. Un autre modèle (ou ce même modèle mieux entraîné !) peut utiliser différemment les variables.
• Il faut faire attention aux variables corrélées !

La question d’interprétabilité des modèles de machine learning est encore ouverte, et c’est un domaine actif en recherche. Les variables corrélées, très courantes en pratiques, rendent plus difficiles les explications. Les importances de variable permettent cependant de mieux comprendre les résultats d’un modèle, et cette étape est nécessaire dans la pipeline globale ML, au même titre que l’analyse des données.