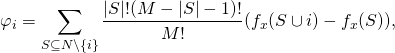SHAP
L’interprétation de modèles de Machine Learning (ML) complexes, encore appelés modèles ”black box”, est aujourd’hui un enjeu important dans le domaine de la Data Science. Prenons l’exemple du dataset « Boston House Prices » [1] où l’on souhaite prédire les valeurs médianes de prix de logements par quartier de la ville de Boston en fonction de critères tels que le nombre de pièces, la proximité à un centre d’emplois, etc. Par un modèle de ML nous pouvons effectivement prédire ces valeurs pour chaque quartier. Cependant, cette prédiction n’apporte pas d’informations sur les paramètres qui ont influencés chaque valeur prédite. Par ailleurs, nous devons être capables d’expliquer les prédictions, notamment dans les cas listés ci-dessous :
- Aspect légal : L’article 22 du RGPD prévoit des règles pour éviter que l’homme ne subisse des décisions émanant uniquement de machines. Les modèles sans explication risquent d’entraîner une sanction qui peut s’élever à 20 000 000 d’euros ou, dans le cas d’une entreprise, à 4% du chiffre d’affaires mondial total de l’exercice précédent (le montant le plus élevé étant retenu),
- Validation du modèle : Le modèle a une bonne précision, mais nous cherchons à connaître les variables influentes afin de vérifier la cohérence avec la connaissance métier du domaine. D’autre part, pour certaines applications, nous devons également contrôler le risque du modèle, ce qui nécessite une compréhension approfondie de celui-ci,
- Explication et recommandation : Imaginons le client d’une banque faisant une demande de prêt, la demande est refusée suite à la décision d’un modèle de ML. Il faut cependant pouvoir expliquer à ce client les raisons de ce refus afin de pouvoir le conseiller.
Z. C. Lipton [2] classe les approches d’interprétation de modèles en deux grandes catégories :
- Comprendre les mécanismes de fonctionnement du modèle,
- Extraire des informations du modèle.
Nous allons ici nous concentrer sur ce deuxième aspect, et plus précisément sur l’interprétation locale de modèle.
Pour extraire des informations du modèle, la première étape est sûrement l’approche globale qui consiste à définir l’importance des variables du modèle de manière globale. La seconde étape consiste à changer d’échelle afin d’extraire des informations locales pour des exemples spécifiques de notre dataset (figure 1). Nous allons revenir sur ces différents points par une approche proposée par Lundberg et al. [4], utilisant la valeur de Shapley.
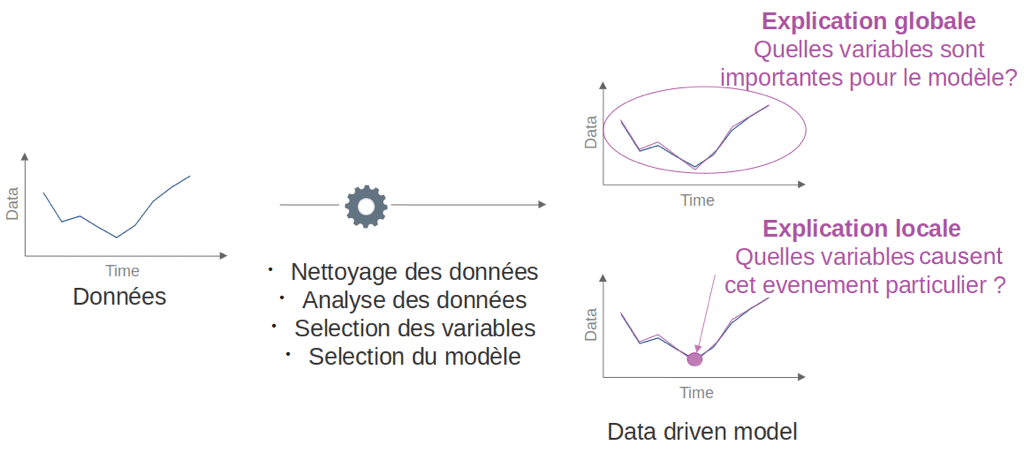
Figure 1 : Importance des variables dans le modèle. Deux échelles d’étude, niveau global du modèle et niveau local d’un exemple spécifique que l’on cherche à expliquer
SHAP par S. Lundberg
La valeur de Shap proposée par Lundberg et al. [4] est la valeur SHapley Additive exPlanation. L’idée proposée par ces auteurs est de calculer la valeur de Shapley pour toutes les variables à chaque exemple du dataset. Cette approche explique la sortie d’un modèle par la somme des effets ![]() de chaque variable Xi. Ils se basent sur la valeur de Shapley qui provient de la théorie des jeux. L’idée est de moyenner l’impact qu’une variable a pour toutes les combinaisons de variables possibles.
de chaque variable Xi. Ils se basent sur la valeur de Shapley qui provient de la théorie des jeux. L’idée est de moyenner l’impact qu’une variable a pour toutes les combinaisons de variables possibles.
Ils ont démontré que cette approche respectait les trois propriétés suivantes :
- Additivité : la somme des effets des variables est égale à la prédiction du modèle pour tous les exemples,
- Variables nulles sans effet : si une variable de l’exemple considéré est à zéro, alors la variable ne doit pas avoir d’impact pour cet exemple,
- Cohérence : si un modèle change, tel que l’effet d’une variable est plus important sur le modèle, l’attribution assignée à cette variable ne doit pas baisser.
L’expression générale de la valeur de Shapley ![]() est :
est :
Avec ![]() le nombre de variables,
le nombre de variables, ![]() un ensemble de variables,
un ensemble de variables, ![]() la fonction de prédiction à l’instant
la fonction de prédiction à l’instant ![]() ,
, ![]() ,
, ![]() est la
est la ![]() variable.
variable.
L’approche SHAP est additive, donc une prédiction peut être écrite comme la somme des différents effets des variables (valeur de shap ![]() ) ajoutée la valeur de base
) ajoutée la valeur de base ![]() . La valeur de base étant la moyenne de toutes les prédictions du dataset:
. La valeur de base étant la moyenne de toutes les prédictions du dataset:
(2) 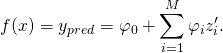
Avec, ![]() la valeur prédite du modèle pour cette exemple,
la valeur prédite du modèle pour cette exemple, ![]() la valeur de base du model,
la valeur de base du model, ![]() quand la variable est observée
quand la variable est observée ![]() ou inconnue
ou inconnue ![]() .
.
Grâce à la valeur de Shap, on peut déterminer l’effet des différentes variables d’une prédiction pour un modèle qui explique l’écart de cette prédiction par rapport à la valeur de base. La figure 2 décrit les outputs d’une fonction par la somme des ces effets (la figure provient de l’article [3]).

Figure 2 : Valeurs de Shap [3]. Prédiction f(x) expliquée par la somme des effets ![]() de chaque variable
de chaque variable
Aussi, en moyennant les valeurs absolues des valeurs de Shap pour chaque variable, nous pouvons remonter à l’importance globale des variables.
TreeExplainer
La valeur de Shap est très coûteuse à calculer et c’est un désavantage de cette approche. Cependant, les auteurs de [4] ont développé un algorithme appelé TreeExplainer, optimisé pour les arbres de décision et ensembles d’arbres, qui permet de passer d’une complexité en ![]() à
à ![]() . Avec
. Avec ![]() le nombre d’arbres,
le nombre d’arbres, ![]() le maximum de nombre de feuilles des arbres,
le maximum de nombre de feuilles des arbres, ![]() le nombre de variables et
le nombre de variables et ![]() la profondeur maximale des arbres.
la profondeur maximale des arbres.
Cette approche va utiliser la construction des arbres afin de réduire les coûts de calcul. L’algorithme récursif va garder en mémoire tous les ensembles possibles de variables qui descendent dans chaque feuille de l’arbre, et pour chaque exemple les valeurs des feuilles, la proportion d’exemples et les chemins des « hot » et « cold child » sont utilisés pour l’estimation des valeurs de Shap. Pour plus de détails sur l’algorithme, vous pouvez vous référer à l’article [4].
Shap par l’exemple
Voici un exemple de l’utilisation de Shap sur le dataset de Boston House Prices [1].

Figure 3 : Importance globale des variables en utilisant les valeurs de Shap. Sur l’image de gauche, l’importance des variables est calculée en moyennant la valeur absolue des valeurs de Shap. Sur la droite, les valeurs de Shap sont représentées pour chaque variable dans leur ordre d’importance, chaque point représente une valeur de Shap (pour un exemple), les points rouges représentent des valeurs élevées de la variable et les points bleus des valeurs basses de la variable
La figure 3 représente l’importance globale des variables calculées par les valeurs de Shap. Grâce au fait que les valeurs sont calculées pour chaque exemple du dataset, il est possible de représenter chaque exemple par un point (figure de droite) et ainsi avoir une information supplémentaire sur l’impact de la variable en fonction de sa valeur. Par exemple LSTAT qui est la variable la plus importante, a un impact négatif quand la valeur de cette variable est élevée.

Figure 4 : Explication d’impact des variables pour deux exemples du dataset. En rouge, les variables qui ont un impact positif (contribuent à ce que la prédiction soit plus élevée que la valeur de base) et, en bleu, celles ayant un impact négatif (contribuent à ce que la prédiction soit plus basse que la valeur de base)
Sur la figure 4, deux exemples ont été représentés. La valeur de base du dataset est à 22,6 (moyenne des valeurs des prix des logements des quartiers), la prédiction de la valeur médiane des logements par zones de la première zone étudiée dans l’exemple est 31,52 et de la deuxième 39,32. Nous étudions donc deux exemples de quartiers qui ont une prédiction de valeur plus élevée que la moyenne, nous voyons cependant que les raisons du modèle pour lesquelles les valeurs sont plus élevées sont différentes (contribution positive de LSTAT et RM pour le premier et contribution positive de LSTAT et DIS pour le deuxième).
Pour aller encore plus loin
Clustering : S. Lundberg [3], propose aussi de regrouper les exemples similaires par clustering en utilisant les valeurs de Shap.
Interactions : De la même manière que nous avons calculé les valeurs de Shap pour chaque variable, nous pouvons calculer les valeurs de Shap pour des couples de variables et étudier les interactions de variables entre elles.
Comparaison : Du fait que la valeur de base de Shap reste la même pour tout le modèle et que cette approche soit additive, nous pouvons aisément comparer les effets des variables pour différents exemples. Effectivement, entre deux exemples qui ont des prédictions différentes, la comparaison des effets des variables peut apporter de nouvelles informations sur les variations relatives des effets.
Conclusion
TreeExplainer de Shap permet d’accéder avec un temps de calcul raisonnable à une approximation des valeurs de Shapley dans le cas de modèles d’arbre de décision ou d’ensembles d’arbres. Par cette approche, nous pouvons calculer l’importance globale des variables mais surtout les effets des variables pour chaque exemple du dataset. Dans cet article, sur le dataset Boston House Prices [1], nous avons expliqué, grâce au modèle Shap, l’importance des variables au niveau global du modèle mais aussi pour chaque exemple spécifique du modèle. Nous avons ainsi pu comparer deux quartiers avec des prix de logements élevés selon le modèle et nous avons montré que les raisons pour lesquelles le modèle a attribué une valeur élevée à ces quartiers sont différentes.
Pour résumer cette approche nous pouvons :
- Étudier les importances globales et locales des variables,
- Expliquer les prédictions d’un modèle,
- Comparer deux exemples,
- Regrouper les exemples par similarité des effets des variables,
- Étudier les interactions des variables.
Il est ainsi possible de confronter les modèles aux connaissances du domaine étudié afin de vérifier la cohérence, mais aussi d’apporter des explications sur des prédictions spécifiques.
par Anita Dehoux & Clément Liao