Gérer le déséquilibre des classes dans un jeu de données

Retrouvez toutes nos autres videos sur notre chaîne YouTube. 

Toutefois, en Data Science, on désignera par cette appellation les jeux de données où l’une des classes (ou plusieurs) est extrêmement minoritaire par rapport aux autres. Par exemple, un dataset où 98% des données appartiennent à la classe “A” contre seulement 2% à la classe “B” est un dataset fortement déséquilibré.

La notion de “déséquilibre de classe” est très importante en machine learning, et en particulier pour les modèles de type “supervisés” qui impliquent deux classes (ou plus)

1. Pourquoi est-ce important ?

En règle générale, la plupart des modèles fonctionnent correctement si les proportions des classes dans un dataset sont relativement similaires : les légers déséquilibres de classes sont bien gérés.  Cependant, passé un certain point, les modèles de machine learning auront du mal à identifier correctement la (ou les) classe(s) minoritaire(s). C’est une situation pourtant fréquente, rencontrée dans une variété de problèmes réels : détection de fraude ou de défauts, diagnostic médical, etc.

Si l’on reprend l’exemple typique de la classification d’emails frauduleux (de type spam, arnaque, hameçonnage, malwares, etc.), alors seulement une très faible proportion d’entre eux s’avèrent être frauduleux. Ce type d’emails est donc rare dans les datasets, et les modèles ont du mal à les classifier : ils apprennent un biais vis-à-vis de la classe majoritaire (email “non frauduleux”), et ont alors tendance à toujours prédire cette dernière.

L’accuracy (ou “précision” en français, à ne pas confondre avec la “precision” en anglais qui désigne une autre métrique), est une mesure souvent utilisée comme indicateur de performance. Toutefois, elle est contre-indiquée pour les datasets déséquilibrés : il sera en effet très facile d’obtenir un très bon score d’accuracy sur ce type de dataset, sans pour autant que les modèles n’aient appris quoique ce soit, si ce n’est que de jouer la sécurité en prédisant toujours la classe majoritaire ! Cette métrique peut donc se révéler trompeuse car elle ne reflétera pas l’état d’apprentissage du modèle.

2. Les différentes étapes et/ou méthodes à suivre

Il existe plusieurs méthodes pour pallier à un déséquilibre des classes dans un dataset. Nous les présentons ici ainsi que quelques conseils :

Tout d’abord, il convient de vérifier que le déséquilibre du dataset soit représentatif de ce que l’on s’attend à trouver dans la réalité, et donc des données que l’on présentera à un modèle mis en production. En d’autres termes, il faut s’assurer que la distribution des données ne provient pas d’un “artifice” tel par exemple un mauvais filtrage en amont des données (lors des phases de collecte des données ou de nettoyage par exemple). Si oui, il peut alors être intéressant de voir s’il n’est pas possible de collecter plus de données : par exemple, dans le cas de données temporelles, est-ce que le fait d’aller plus loin dans le passé nous permet d’augmenter la proportion des classes minoritaires ? Ou bien est-ce que l’un des filtres appliqués en amont lors de la phase de data cleaning ne supprimerai-il pas particulièrement telle ou telle classe ?

Il peut aussi être possible de regrouper les classes minoritaires en une classe unique si ces dernières présentent des similarités. Et, si une classification plus précise des classes minoritaires est réellement nécessaire, il sera toujours possible de réentraîner un autre modèle, en aval, sur les prédictions du premier modèle. Cette solution, qui implique l’entrainement de deux modèles distincts, peut parfois s’avérer être la solution la plus simple.

Il est très important de choisir une métrique adaptée à ce type de problème, car comme nous l’avons vu plus haut, la mesure de l’accuracy n’est pas suffisante. Pour clarifier les idées au niveau de ces mesures, nous introduisons certains termes ici :

• • True Positive (TP) : ce sont les observations positives qui ont été prédites correctement par le modèle (ou pour simplifier, les observations prédites comme étant “oui” et étant véritablement “oui”).
  • True Negative (TN) : de manière similaire, ce sont les observations négatives correctement prédites par le modèle (les observations prédites comme “non” et étant réellement “non”).
  • False Positive (FP) : ce sont les observations négatives prédites (de manière erronée) par le modèle comme étant positives (un vrai “non” prédit comme un “oui”).
  • False Negative (TN) : ce sont les observations positives prédites comme étant négatives par le modèle (un vrai “oui” prédit comme un “non”).

L’accuracy, qui est la mesure de performance d’un modèle la plus intuitive, peut être définie à partir de ces termes : il s’agit tout simplement du ratio des observations correctes prédites sur le total des observations, soit : . C’est une métrique très efficace dans le cas de dataset équilibrés.

Pour les datasets déséquilibrés, les métriques couramment utilisées pour mesurer la performance des modèles sont :

• La combinaison de la Precision, du Recall, et du F1-score :
  • La Precision est le ratio des observations prédites positives correctement sur le total des observations prédites positives tout court, soit : 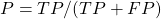. Cette métrique permet de voir à quel point nos prédictions positives tombent “juste”.
  • Le Recall (ou Sensitivity) est le ratio des observations prédites positives correctement sur l’ensemble des observations réellement positives, soit : 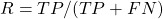. Cette métrique permet de mesurer à quel point l’on capture tous les vrais positifs dans nos prédictions.
  • Le F1-score est une moyenne pondérée de la Precision et du Recall. Son expression est : 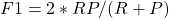. Cette métrique est en générale plus utile que l’accuracy, car elle prend en compte à la fois les faux positifs et les faux négatifs.
• Les matrices de confusions sont des tables qui permettent de visualiser la performance d’un modèle en affichant les mesures des TP, TN, FP, et FN. Toutes les observations qui se situent sur la diagonale de la matrice ont été correctement prédites par le modèle, tandis que les observations qui ne se situent pas sur la diagonale correspondent à des erreurs du modèle. Un modèle parfait aurait donc l’ensemble de ses prédictions sur la diagonale d’une matrice de confusion.

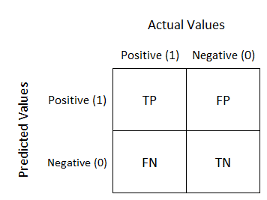
Source : Understanding Confusion Matrix by Sarang Narkhede on Towards Data Science

Rien de tel qu’une illustration pour bien fixer les idées :

• L’AUC (Area Under the Curve) ROC (Receiver Operating Characteristic) curve, souvent abrégée en AUROC, est également une métrique très utile. La ROC curve, aussi appelée courbe de sensitivité/spécificité, est une courbe de probabilité qui permet de visualiser la performance des modèles de classification. Il s’agit ici simplement du taux des True Positive (TPR) tracé en fonction du taux des False Negative (FPR). L’AUC, comprise entre 0 et 1, va elle représenter une mesure du degré de séparabilité des prédictions du modèle : un modèle avec une AUC proche de 1 prédira le plus souvent correctement les 0 comme des 0 et les 1 comme des 1. Un modèle “parfait” aurait donc une ROC curve en forme de “L” inversé, qui commencerait par suivre parfaitement l’axe des TPR, puis serait horizontale lorsque le TPR vaut 1 (car l’air sous cette courbe vaut 1).

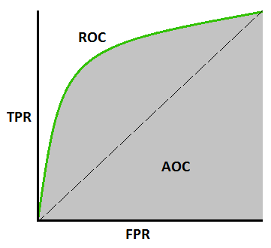
Source : Understanding AUC-ROC curve by Sarang Narkhede on Towards Data Science

• Le test non paramétrique Kappa de Cohen, ou Cohen’s Kappa accuracy [Cohen], est une mesure statistique de l’accord entre deux ou plusieurs annotateurs internes (c’est à dire deux “voteurs” ou “juges”) lorsque les décisions sont qualitatives. Pour prendre un exemple concret, si nous souhaitons mesurer l’accord entre deux banquiers qui classifieraient 100 clients de manière binaire, alors il faudrait utiliser le coefficient de Kappa pour quantifier leur “accord”. Cette métrique, qui mesure la reproductibilité pour des variables aléatoires non continues, permet donc de contrôler quelles sont les observations qui ont été correctement classifier uniquement par chance pour essayer d’y remédier. Elle est calculée, pour deux observateurs statistiquement indépendants, à partir de la formule suivante : 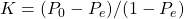où :
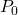  • est la proportion d’accord observé (l’accuracy donc)
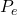  • est la proportion d’accord aléatoire sous l’hypothèse d’indépendance des jugements (autrement dit une accuracy “aléatoire”)

Pour un développement plus détaillé de cette métrique, vous pouvez vous référer à l’excellent article Cohen’s Kappa : What is it, when to use it, and how to avoid its pitfall de Maarit Widmann.

• Il est également important de choisir un algorithme qui soit adapté à de tels datasets. Les arbres de décisions, et les modèles pénalisés, où une pénalité est ajoutée lorsqu’une classe minoritaire est mal prédite (forçant alors le modèle à y accorder plus d’attention), sont particulièrement efficace à gérer ce type de problèmes. Nous détaillerons plus bas comment construire un modèle pénalisé par la méthode des class weights.

Enfin, un modèle de type “détection d’anomalie” peut s’avérer bien plus adapté qu’un classificateur classique s’il n’y a que deux classes.

• Il est également conseillé de ré-équilibrer le dataset. En fonction de la quantité de données disponible, on choisira alors l’une ou l’autre des méthodes suivantes :
  • L’undersampling lorsque l’on dispose d’un très grand nombre d’observations (à minima > 10K). Il s’agit ici simplement de retirer aléatoirement des instances de la classe majoritaire afin de ré-équilibrer les proportions. On perd toutefois de l’information, et il y a donc un risque d’underfitting.
  • L’oversampling lorsque l’on dispose d’un nombre limité d’observations (< 10K), ou bien si le temps de calcul n’est pas un problème. Il s’agit ici de dupliquer aléatoirement certaines instances des classes minoritaires, rendant ainsi leur signal plus puissant. Il y a toutefois ici un risque d’overffiting.
  • La méthode des class weights permets de prendre en compte le caractère biaisé de la distribution du dataset et de créer un modèle pénalisé. Il s’agit ici de simplement attribuer des poids différents aux différentes classes de notre dataset, en donnant un poids plus important aux classes minoritaires, afin d’influencer le modèle lors de son entraînement. Nous pénalisons ainsi plus fortement une erreur de classification d’une classe minoritaire par rapport à une erreur de classification d’une classe majoritaire.

Il est à noter que la plupart des modèles disponibles dans la librairie scikit-learn ont un paramètre “class_weight” qui est par défaut initialiser à None, donnant alors des poids égaux pour toutes les classes. En mettant ce paramètre à “balanced”, nous pouvons indiquer à scikit-learn de calculer automatiquement les poids pour chaque classe. Ces poids sont calculés comme étant inversement proportionnels à la fréquence de la classe minoritaire. La formule est :

où :

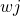• est le poids de la classe j
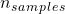• est le nombre total d’observations dans le dataset
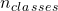• est le nombre de classes présentes dans le dataset
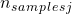• est le nombre total d’instances de la classe j

Il est aussi possible de donner à scikit-learn un dictionnaire où les poids ont été entrés manuellement.

• • La génération de données synthétiques. Les deux options les plus fréquentes sont :
    • La Data augmentation sur les classes minoritaires, qui est en soit une forme d’oversampling.
    • La génération de données par des algorithmes. Les plus connus proviennent de SMOTE (pour Synthetic Minority Over-sampling Technique) et de ses variantes [Chawla]. Le principe est relativement simple : l’algorithme va sélectionner une instance de la classe minoritaire, puis regarder quelles sont les k (typiquement k=5) instances de la classes minoritaires les plus proches de l’instance choisie dans l’espace latent, et en sélectionner une aléatoirement. A partir de là, une instance synthétique est créée en traçant aléatoirement un nouveau point le long de la ligne reliant ces deux observations.

A noter que la librairie imbalanced-learn donne des implémentations toutes faites de ces algorithmes. Pour plus de détailssur la façon d’utiliser SMOTE avec Python, nous vous renvoyer vers l’article SMOTE for Imbalanced Dataset with Python de Jason Brownlee.

Pour des informations complémentaires sur la façon de travailler avec des dataset déséquilibrés, vous pouvez également vous référer à l’article How to deal with imbalance data de Numal Jayawardena.

Nous allons dans la suite appliquer ces conseils à un premier use-case : la classification de commentaires toxiques.

3. Exemple de use-case : classification des commentaires toxiques

Ce use-case est tiré de la compétition Kaggle Toxic Comment Classification Challenge. Le but de cette compétition était la construction de modèles permettant de différencier les types de commentaires toxiques parmi de “bons” commentaires. Les types de toxicité sont : l’obscénité, les menaces, les insultes, les commentaires haineux, les commentaires toxiques et les commentaires très toxiques. Un notebook, dont sont tirées les illustrations et le code présenté dans cette section, est disponible ici.

Premièrement, regardons la distribution de la longueur des commentaires dans le dataset :

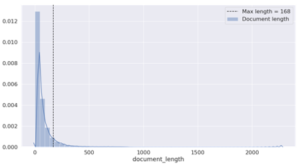
Cela nous permet de définir une longueur maximale pour chaque observation, max_len, que nous choisissons comme étant : max_len = mean + std. Ici, max_len = 168.

Voyons quels sont les mots les plus fréquents dans les classes minoritaires de notre dataset :

Tout cela n’est pas très joli, heureusement, notre classificateur va nous permettre de filtrer les commentaires contenant ces mots.

Voyons quelle est la distribution des classes minoritaires dans le dataset :

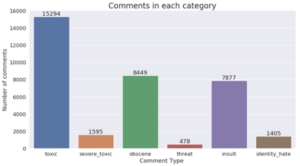
La taille du dataset est de 159 571 observations. La classe minoritaire ”toxic”, pourtant la plus importante des classes minoritaires, est donc 10 fois moins fournies que les commentaires ”bons”. On constate en outre ici un très fort déséquilibre au sein même des classes minoritaires, avec par exemple environ 32 fois moins de commentaire de type ”threat” que de type ”toxic”.

Nous sommes en outre ici face à un problème de classification multi-label : un seul et même commentaire peut correspondre à plusieurs types de toxicités. Nous le vérifions sur la figure suivante :

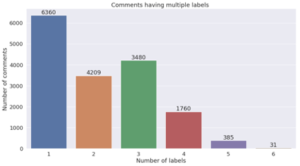
Les problèmes multi-label avec une fort déséquilibre de classes sont particulièrement compliqués à traiter : ici, l’undersampling des observations de la classe majoriataire uniquement ne permet pas d’obtenir de modèle très performant, car même en supprimant aléatoirement une grande partie de sa population, le dataset resterait fortement déséquilibré à cause du déséquilibre présent entre les classes minoritaires.

L’oversampling est donc une meilleure alternative ici, mais la difficulté réside alors dans le fait d’augmenter à la fois les populations des labels minoritaires tout en conservant la distribution des observations multi-labels. Or, ces observations multi-labels sont pour certaines extrêmement minoritaires, et le risque d’overfitting est donc très élevé.

La meilleure alternative serait donc de générer des observations synthétiques afin d’augmenter notre dataset, mais il n’est pas immédiat d’utiliser directement SMOTE sur ce type de problème, car cet algorithme se limite aux problèmes multi-classe dans imbalanced-learn. Notons toutefois qu’une généralisation au cas multi-label existe [Charte].

C’est pourquoi nous allons utiliser ici un modèle supervisé de type pénalisé, que nous évaluerons grâce à l’AUROC et à une matrice de confusion.

Nous passons par la suite sous silence les étapes de data cleaning et de tokenization des commentaires. Si ces dernières vous intéressent, elles sont disponibles dans le notebook. Rapidement, elles consistent en :

• Le chargement de GloVe (une représentation vectorielle d’un vocabulaire, ici 400 000 mots.)
• La suppression des stopwords présents dans notre dataset
• La tokenization du dataset: un index ordonné par la fréquence d’occurence des mots est créé pour chaque mot du dataset  (avec l’index 0 réservé pour le padding). Puis, chaque texte est converti en une suite d’entier selon le dictionnaire des index obtenu précédemment, et compléter par des 0 si la longueur du texte est inférieure à max_len.
• La création d’une matrice d’embedding à partir de GloVe, avec une initialisation aléatoire, basée sur la même moyenne et déviation standards que les mots dans GloVe, pour tous les mots qui ne sont pas présents dans GloVe mais présent dans le dataset.

Pour calculer les différents poids de chaque label, nous utilisons la fonction “compute_class_weight” de sklearn avec le mode “balanced” :

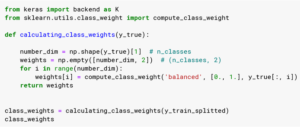
Observons le résultat obtenu :

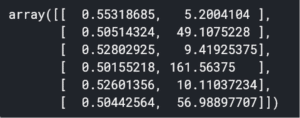
class_weights[:, 0] est un array avec les poids pour le background (les “bons” commentaires”), tandis que class_weights[:, 1] est un array qui contient les poids pour les signaux (les classes minoritaires). Ici, on peut par exemple voir qu’une instance de “threat” à un poids de 161.5 bien plus important que le poids d’un commentaire “bon” qui est à 0.5.

Il nous est maintenant possible de définir notre propre fonction de coût qui prendra en compte ces informations lors de la phase d’entraînement de notre modèle :

L’évaluation du modèle est faite avec l’AUROC :

Le modèle choisi est un modèle Bi-LSTM pré-entrainé sur GloVe avec dropout :

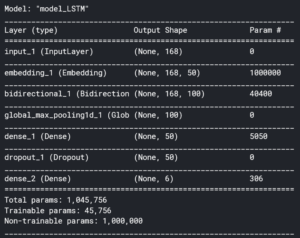
Nous entraînons le modèle sur 6 époques avec des batch de taille 128. Les autres hyperparamètres sont un learning rate de 1e-3 et un optimizer de type adam [Kingma].

L’évaluation du modèle (sur un set de test de 14362 observations) avec l’accuracy_score de sklearn, adaptée au problème multi-label, est de 0.90%

Nous obtenons la matrice de confusion suivante :

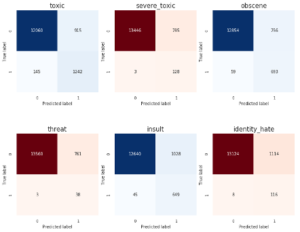
Compte-tenu de la difficulté du problème posé, les résultats sont déjà très bons.

Nous voyons en outre ici l’un des avantages de travailler avec un modèle pénalisé sur ce problème particulier : en effet, avec le mode “balanced” de compute_class_weight, nous capturons la majeure partie des observations positives (plus grand recall) en sacrifiant toutefois la precision (plus de faux positifs). Dans le cadre de la détection/classification de commentaires sur internet, ce comportement est celui qui est attendus : il vaut mieux en effet capturer tous les commentaires nocifs, quitte à en supprimer quelques bons.

Notre modèle possède cependant une large marge de progression, mais pose toutefois une première baseline.

4. Exemple de Use-case à Aquila

De nombreux projets à Aquila nécessitent que nous prenions en compte ces déséquilibres de classes. Pour donner quelques exemples concrets, cela a été le cas pour :

• La prédiction de remboursements anticipés pour des prêts. Nous étions ici face à un problème de classification binaire où les observations positives ne représentaient que 5% du dataset.
• Des projets d’analyse de sentiments, où certaines émotions cherchées sont particulièrement minoritaires
• Des projets de détection de défauts (sur des éoliennes, des panneaux photovoltaïques, des légumes pour l’industrie agro-alimentaire, des rails de chemin de fer, du matériel médical ou spatial, etc.)

Conclusion

Les déséquilibres de classes arrivent très fréquemment dans le monde réel, et il est vital de les prendre en compte afin d’adapter la méthode d’entraînement d’un modèle de Machine Learning. Sans cela, le modèle résultant serait biaisé vis-à-vis de la (ou des) classes(s) majoritaire(s).

Nous avons présenté dans cet article plusieurs techniques, méthodes et métriques à utiliser lorsque l’on est face à ce type de situation. Ensemble, ces dernières forment une boîte à outils qui vous sera certainement utile lorsque vous serez confronté un dataset déséquilibré. Toutefois, rappelons que cette liste est loin d’être exhaustive, et qu’une grande partie du travail d’un data scientist est la recherche de nouvelles solutions qui adaptent l’existant par une succession d’essais/erreurs : il ne faut surtout pas avoir peur d’expérimenter afin de trouver ce qui marche le mieux sur votre problème.

Enfin, il est utile de rappeler de toujours utiliser les mêmes métriques lorsque vous chercherez à comparer vos modèles.