Retrouvez toutes nos autres videos sur notre chaîne YouTube.
Les modèles physiques couplés avec du Machine Learning permettent de valoriser notre connaissance physique du système ainsi que la variété des données que l’on a à notre disposition. En géosciences, les modèles les plus utilisés sont des modèles numériques (approximation d’équations physiques) qui nous permettent d’appréhender le sous-sol ainsi que la dynamique des écoulements des fluides dans le milieu souterrain. Cependant, ces modèles restent des approximations de cas complexes et ne permettent pas de représenter le système dans sa globalité. Les modèles data driven permettent d’incorporer des informations complémentaires quand les systèmes présentent une complexité trop grande. Ces modèles data driven, régis par des lois statistiques, découvrent la structure et les motifs dans les problèmes où la complexité est trop grande et dont on ne connaît pas les lois physiques.
Un modèle physique est un modèle interprétable, qui permet d’identifier les relations causales et dont on a la possibilité de générer des données en réalisant diverses expériences de simulation numériques. Cependant, il ne peut donner qu’une approximation des cas complexes et ne simule que les lois physiques connues. Un modèle data driven permet lui d’inclure toutes les données et n’est pas contraint par la compréhension humaine du système physique. Ce modèle, par des lois purement statistiques et non physiques, peut identifier des relations et motifs non compris. Par ailleurs, il est moins coûteux en temps de calcul par rapport au modèle physique. Cependant il peut violer les lois physiques, ne comprend pas les relations causales et est donc difficile à interpréter.
Coupler ces 2 modèles permet de créer un modèle robuste comportant les avantages des 2 et minimisant leur faiblesse respective.
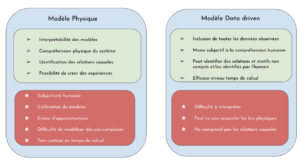
Figure 1 : Comparaison modèle physique et modèle data driven.
Les avantages et faiblesse du modèle (vert et rouge respectivement).
Les modèles numériques physiques consistent à approximer (par des méthodes différences finies, éléments finis..) des équations différentielles physiques bien connues. Elles permettent de simuler en chaque point de l’espace défini (sur un maillage) et en chaque pas de temps des variables en se basant sur des lois physiques. Un modèle physique est un modèle simplifié de la réalité qui permet de prédire l’évolution temporelle et spatiale d’un système à partir de conditions aux frontières, initiales et de lois d’évolution physique connues. Un modèle physique est un modèle qui permet de résoudre, sur un domaine donné, une théorie qui existe déjà ou de retrouver des lois physiques régissant un système.
Nous avons deux types de configurations :
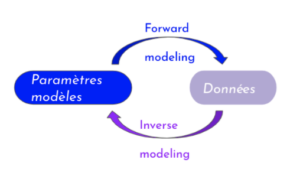
Figure 2 : Modèle direct (forward modeling) et modèle inverse
- Un modèle physique dit direct (Forward modeling) est un modèle qui à partir de paramètres définis préalablement prédit des variables d’état (par e.g dans un modèle d’écoulement de fluide, on donne la perméabilité comme paramètre et la variable prédite est la vitesse de fluide). Ainsi à partir d’un modèle direct, à partir d’un état du système bien défini, on obtient des données.
- Un modèle inverse, lui, part des observations et données simulées par le modèle, pour ajuster les paramètres qui caractérisent le modèle (état du système).
Je vous présente dans cet article comment réaliser techniquement des “MPA” (Modèle Physique Augmenté) et des “MAIAP” (Modèle AI Augmenté Physique) avec des cas d’applications en géoscience.
1 – “Modèle Physique Augmenté” grâce à l’IA
Une première approche, la plus utilisée et la plus directe, consiste à utiliser des données synthétiques (fournies par des modèles physiques dans la configuration directe (Forward modeling)) pour alimenter nos modèles de ML/DL. Ce type d’approche est très utilisé, lorsque l’on manque de données pour entraîner nos modèles.
Chez Aquila Data Enabler, par exemple, nous avons utilisé des résultats de jeux vidéos pour la détection d’EPI. Ce type d’approche est aussi très utilisée dans le cas des problématiques de tomographie.
L’estimation des paramètres pour caractériser le modèle est un problème inverse. Les méthodes inverses utilisant les simulations physiques sont très coûteuses en temps de calcul et ne capturent pas les phénomènes non expliqués par l’humain.
Les modèles de ML/DL pour la paramétrisation sont une méthode moins coûteuse d’une part, et d’autre part qui permet d’intégrer plus d’informations à notre disposition.
Ainsi une seconde approche serait de paramétriser les modèles physiques (au lieu de réaliser des méthodes inverses) grâce à des modèles de machine learning.
Cela permet d’apprendre de nouveaux paramètres directement des observations.
Cette solution est très pertinente notamment pour les problèmes de modélisation de transport réactif ([4]) dans les milieux poreux où les constantes d’équilibre chimique qu’il est nécessaire de calculer sont très coûteuses en temps de calcul. Ainsi, pour pallier à cette contrainte, on fait appel à une approche data driven.
Pour calculer ces constantes, une base de données de ces constantes d’équilibres a été constituée avec les features correspondantes (T, P, etc.).
Une fois cette base de données construite, la nouvelle constante est calculée en fonction de cette base de données :
- si les paramètres sont très proches de ceux dans la database, la constante est prise dans la base de données,
- sinon la nouvelle constante est calculée avec une méthode de ML
Ainsi avec cette approche, on estime ces paramètres à l’aide d’une méthode ML et on le couple à une méthode numérique physique de simulation de fluide.
2 – “Modèle AI Augmenté” (Modèle AI guidé par des contraintes physiques)
Une autre approche de couplage serait de créer un modèle de réseau de neurones en y intégrant notre connaissance physique a priori.
Mais avant de rentrer dans le détail, revenons rapidement sur ce que l’on nomme les réseaux de neurones.
Un réseau de neurones permet d’extraire les motifs non linéaires des données…
Il en existe 2 grands types :
- Les réseaux convolutionnels (CNN)
- Les réseaux récurrents (RNN)
Les réseaux convolutionnels se focalisent sur l’extraction de motifs spatiaux alors que les réseaux récurrents récupèrent les motifs temporels.
Ces réseaux sont composés de plusieurs couches de neurones, et calculent à la sortie des poids qui décrivent le modèle à représenter.
Ces poids sont calculés en minimisant une fonction objective (fonction loss) de façon similaire à ce que l’on fait en méthode inverse pour ressortir une estimation des paramètres.
Dans la démarche usuelle, cette fonction loss consiste à minimiser la différence de la valeur prédite et la vraie valeur de la variable cible (encore une fois similairement aux méthodes inverses).
Cependant, si nous voulons rajouter une information physique dans notre modèle de Deep Learning, il est important d’introduire une contrainte physique.
La manière la plus courante est d’intégrer un terme de régularisation dans la fonction LOSS .
![]()
Un cas d’application pourrait être les modèles d’écoulement de fluide. En effet, dans ce cas, la conservation de masse se traduit de la façon suivante :
![]()
Avec
![]() ,
, ![]()
avec les conditions aux frontières suivantes (type Dirichlet et Neumann):
![]()
![]()
Par exemple, pour simuler l’écoulement d’un fluide, on crée deux réseaux de neurones, un pour la vitesse de fluide et l’autre pour la perméabilité :
En créant notre modèle de réseau de neurones pour les 2 variables dans leur évolution temporelle et spatiale, on y intègre aussi des contraintes physiques assurant la conservation de masse. Ces contraintes physiques peuvent être intégrées dans la loss.
Dans la loss, on inclut en plus de la différence des données produites, les conditions aux frontières traduisant dans ce cas-là la conservation de masse.
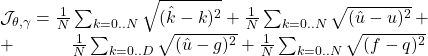
avec
![]()
Sur la première ligne, on minimise l’erreur sur les variables prédites, et sur la deuxième ligne on introduit les 2 types de conditions aux frontières (type Dirichlet et Neumann).
Un autre moyen serait d’ajouter une couche dans notre réseau de neurones, contenant des contraintes physiques.
Un cas d’application à réaliser est la reconstitution de well logs.
Les motifs temporels des signaux sont capturés par le modèle LSTM, et le modèle physique (géomécanique) a priori est introduit dans une couche de réseau de neurone.
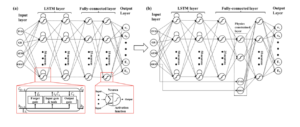
Figure 3 : Modèle de réseau neurones guidé par des principes physiques (loi de géomé-
canique) pour modéliser les composantes mécaniques du sous-sol à l’aide de well logs ([2])
Un autre cas d’application est la prédiction de températures des lacs ([3]).
Dans ce cas, la dynamique temporelle est également capturée par le modèle LSTM . Dans ce modèle récurrent est intégrée la loi de conservation de l’énergie. En effet le transfert d’énergie est une des causes principales au changement de température de surface d’où l’importance d’introduire la loi universelle de la loi de conservation applicable à tous les lacs.
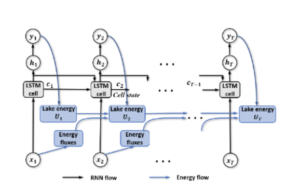
Figure 4 : Modèle de réseau neurones guidé par des principes physiques
(loi de conservationde l’énergie) pour modéliser les températures de lac ([3])
Conclusion
Ainsi combiner ces 2 approches s’avèrent intéressant, car nous pouvons intégrer nos connaissances physiques qui marchent dans les cas dont la complexité est contrôlée, mais aussi bénéficier des avantages des modèles ML/DL qui permettent d’extraire des motifs dont on ne connaît pas la source physique. En couplant ces 2 approches complémentaires, on bénéficie d’une vue plus globale du problème. On peut rapprocher ce type d’approche à un problème de Computer Vision, dans lequel on intègre plusieurs bases de données de différentes perspectives pour avoir une vue complète de l’objet.
Chez Aquila Data Enabler, en couplant nos expertises de physiciens à celles de data scientists, nous nous efforçons de créer des modèles hybrides permettant d’incorporer les connaissances du domaine métier à nos modèles ML/DL. Cela permet de donner du sens et de l’interprétabilité, très importants pour prendre les décisions les plus pertinentes.







