méthodes de prévision
Les séries temporelles, qu’est-ce que c’est ?
Les séries temporelles peuvent être vues comme des séquences de points de données mesurées sur des intervalles de temps successifs. Considérées à tort comme étant une branche exclusive de l’économétrie, les séries temporelles ont été utilisées bien avant cette discipline relativement récente, par exemple en astronomie (1906) et en météorologie (1968).
Leurs principales spécificités par rapport aux domaines les plus courants de l’apprentissage automatique sont leur dépendance dans le temps et leurs comportements saisonniers pouvant apparaître dans leur évolution. Dans le cas de mesures météorologiques, intuitivement, nous comprenons que la température de demain sera affectée par la séquence des jours passés. On dit de ces données qu’elles ne sont donc pas indépendantes.
Avant de parler de comment modéliser ce type de données, il convient de les analyser. Une propriété importante de la série chronologique est sa stationnarité. Si un processus est stationnaire, cela signifie que ses propriétés statistiques ne varie pas dans le temps, à savoir sa moyenne, sa variance (homoscédasticité) ou encore sa covariance.
Alors pourquoi la stationnarité est-elle si importante? Parce qu’il est plus aisé de faire des prédictions sur une série s’il est possible de supposer que les futures propriétés statistiques ne seront pas différentes de celles actuellement observées. La plupart des modèles de prévisions de séries chronologiques, d’une manière ou d’une autre, s’appuie sur ces propriétés (moyenne ou variance, par exemple). Ces pronostics seraient faux si la série originale n’était pas stationnaire. Malheureusement, la plupart des séries chronologiques que nous voyons en dehors des manuels scolaires sont non stationnaires, mais nous pouvons changer cela.
D’où provient la non stationnarité ? Une décomposition très classique d’une série chronologique nous fournit quelques éléments de réponses.
- Tendance
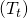 : une tendance correspondant à une évolution de long terme de la série. Elle n’est pas forcément linéaire.
: une tendance correspondant à une évolution de long terme de la série. Elle n’est pas forcément linéaire. - Saisonnalité
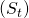 : il s’agit de la propriété d’une série chronologique affichant des comportements périodiques se répétant à une fréquence constante (semaine/ week-end, été/hiver).
: il s’agit de la propriété d’une série chronologique affichant des comportements périodiques se répétant à une fréquence constante (semaine/ week-end, été/hiver). - Cycles
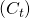 : Les cycles sont des saisons qui ne se produisent pas à fréquence fixe.
: Les cycles sont des saisons qui ne se produisent pas à fréquence fixe. - Bruit
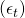 : Le bruit statistique correspond à des fluctuations de nature irrégulières, aléatoires et inexpliquées.
: Le bruit statistique correspond à des fluctuations de nature irrégulières, aléatoires et inexpliquées.
Cette décomposition peut être additive ![]() ou multiplicative
ou multiplicative ![]() . Il est également possible de combiner ces deux décompositions
. Il est également possible de combiner ces deux décompositions ![]() .
.
La prévision de série chronologique trouve une large application dans l’analyse de données. Ce ne sont que quelques-uns des cas d’usage qui pourraient être utiles :
- Météorologie: Prévision de variables météorologiques telles que la température, les précipitations, le vent, etc.
- Economie & Finance: Explication et prévision des facteurs économiques, des indices financiers, des taux de change, etc.
- Marketing: suivi des indicateurs de performance clés des entreprises, tels que les ventes, les revenus / dépenses, etc.
- Télécommunications: prévision des enregistrements de données d’appel, gestion des effectifs des centres d’appel, etc.
- Industrie: Contrôle des variables énergétiques, des journaux efficaces, analyse des sentiments et des comportements, etc.
- Web: sources de trafic Web, clics et journaux, etc.
Vous pensez peut-être que seuls des modèles statistiques simples sont utilisés pour la prévision de séries chronologiques. En fait, il existe de nombreux modèles ou approches complexes qui peuvent être très utiles dans certains cas. L’hétéroscédasticité conditionnelle autorégressive généralisée (GARCH), les modèles bayésiens et les vecteurs ARIMA (VAR) ne sont que quelques exemples. Il existe également des modèles de réseaux neuronaux pouvant être appliqués à des séries chronologiques qui utilisent des prédicteurs retardés ou « laggés ». Il existe même des modèles de séries chronologiques empruntés à l’apprentissage en profondeur, en particulier dans la famille RNN (réseau récurrent de neurones), tels que les réseaux LSTM (mémoire à court et long terme) et GRU (unité récurrente à porte).
Ci-dessous je vous propose de développer un certain nombre de techniques servant à la modélisation des séries temporelles, à commencer par les basiques.
Les températures journalières à Paris au cours de l’année 2017, issue de la réanalyse ERA5 du centre européen pour les prévisions météorologiques, présentés à la figure 1 seront utilisées pour illustrer les différentes méthodologies de prévisions des séries temporelles.
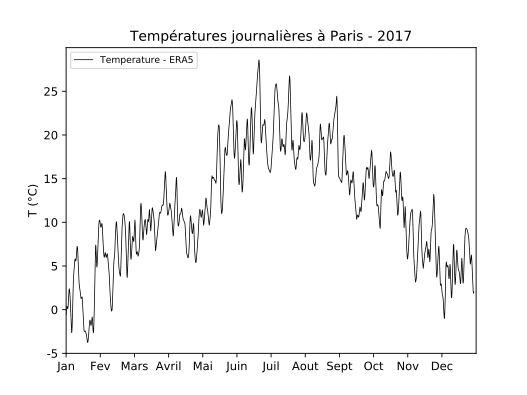
Les méthodes de lissage exponentiel
Les prévisions produites à l’aide de méthodes de lissage exponentielles sont des moyennes pondérées d’observations antérieures, les poids décroissant de manière exponentielle à mesure que les observations vieillissent. En d’autres termes, plus l’observation est récente, plus le poids associé est élevé. Ce cadre génère des prévisions fiables rapidement et pour une large gamme de séries chronologiques. Le lissage exponentiel simple convient pour la prévision de données sans tendance claire ni de tendance saisonnière et pour un horizon de prévision restreint.
Pour comprendre ce type de modèle, commençons donc par une hypothèse naïve et classique, la persistance : « demain sera le même qu’aujourd’hui ». Cependant, au lieu d’un modèle tel que (ce qui est en fait une excellente base pour tout problème de prédiction de série chronologique et parfois impossible à battre), nous supposerons que la valeur future de notre variable dépend de la moyenne de ses k valeurs précédentes. Par conséquent, nous allons utiliser une moyenne glissante.
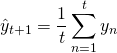
Voyons maintenant ce qui se passe si, au lieu de pondérer les dernières k valeurs de la série chronologique, nous commençons à pondérer toutes les observations disponibles tout en diminuant de façon exponentielle les poids à mesure que nous remontons dans le temps. Il existe une formule pour le lissage exponentiel qui nous aidera avec ceci:
Ici, la valeur du modèle est une moyenne pondérée entre la valeur vraie actuelle et les valeurs du modèle précédent. α est un facteur de poids appelé facteur de lissage compris entre 0 et 1. Il définit la rapidité avec laquelle nous « oublierons » la dernière observation vraie disponible. Plus α est petit, plus les observations précédentes ont d’influence et plus la série est lisse. Le caractère exponentiel est cachée dans la récursivité de la fonction – on multiplie par (1-α) chaque fois, qui contient déjà une multiplication par (1-α) des valeurs du modèle précédent.
Un tel modèle nous permet de prévoir un pas de temps dans le futur. Pour améliorer notre horizon de prévision, basons-nous sur la méthode de Holt-Winters et étendons notre modèle avec deux termes supplémentaires. Ces termes prendront en compte les notions de tendance et de saisonnalité exposées dans l’introduction.
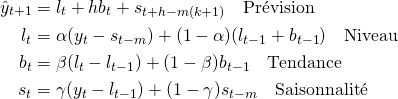
Où :
![]() est la partie entière de (h-1) / m, ce qui garantit que les indices saisonniers utilisés pour les prévisions proviennent de la dernière année de l’échantillon.
est la partie entière de (h-1) / m, ce qui garantit que les indices saisonniers utilisés pour les prévisions proviennent de la dernière année de l’échantillon.
![]() désigne une estimation du niveau de la série à l’instant t.
désigne une estimation du niveau de la série à l’instant t. ![]() est une moyenne pondérée de l’observation corrigée des variations saisonnières
est une moyenne pondérée de l’observation corrigée des variations saisonnières ![]() et de la prévision non saisonnière pour le temps t, donnée ici par
et de la prévision non saisonnière pour le temps t, donnée ici par ![]()
![]() désigne une estimation de la tendance (pente) de la série à l’instant t,
désigne une estimation de la tendance (pente) de la série à l’instant t, ![]() est le paramètre de lissage du niveau, et
est le paramètre de lissage du niveau, et ![]() est le paramètre de lissage de la tendance.
est le paramètre de lissage de la tendance. ![]() et
et ![]() sont compris entre 0 et 1
sont compris entre 0 et 1
La saisonnalité ![]() est modélisée par une moyenne pondérée entre l’indice saisonnier actuel
est modélisée par une moyenne pondérée entre l’indice saisonnier actuel ![]() et l’indice saisonnier de la même saison du cycle (année) précédent
et l’indice saisonnier de la même saison du cycle (année) précédent ![]() .
.
Pour chaque observation de la saison, il est possible d’ajouter une composante distincte. Par exemple si la saisonnalité est hebdomadaire, nous aurons 7 composantes saisonnières, une pour chaque jour de la semaine.
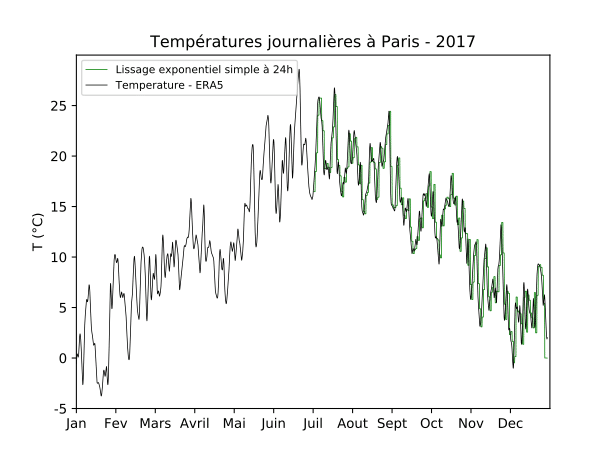
Pour illustrer le lissage exponentiel nous reprenons à la figure 2 les températures en 2017 à Paris. Les prévisions à 24 heures avec le lissage exponentiel sont représentées en vert sur la figure 2 après une calibration sur la première partie de l’année
Les méthodes SARIMA
Les modèles ARIMA (AutoRegressive Integrated Moving Average) offrent une approche complémentaire de la prévision de séries chronologiques. Alors que les modèles de triple lissage exponentiel sont basés sur une description de la tendance et de la saisonnalité dans les données, les modèles ARIMA visent à décrire les autocorrélations dans les données.
Une ARIMA capture donc une suite de différentes structures temporelles. Il s’agit d’une généralisation de la moyenne mobile auto-régressive à laquelle s’ajoute un processus de différenciation afin de rendre la série temporelle stationnaire. La différenciation se calcule par différences entre les observations consécutives.
L’acronyme ARIMA est descriptif et capture bien les aspects clés du modèle lui-même. En bref, ils sont :
- La partie autorégressive prendra en compte les occurrences passées de la série temporelle du modèle. La variable d’intérêt est calculée en utilisant une combinaison linéaire des valeurs antérieures de la variable. Le terme autorégression indique qu’il s’agit d’une régression de la variable par rapport à elle-même. Une autorégression d’ordre peut-être écrit de la sorte :
![]()
- La partie intégrée (I) est le degré nécessaire pour rendre une série temporelle stationnaire, i.e. le nombre de différenciation nécessaire à appliquer sur la série chronologique.
- Plutôt que d’utiliser les valeurs passées de la variable de prévision dans une régression, la partie à moyenne mobile utilise les erreurs de prévision passées dans un modèle de type régression. Elle peut s’écrire de la sorte :
![]()
Le modèle complet peut donc s’écrire :
![]()
Où est la série temporelle différenciée.
L’adoption d’un modèle ARIMA pour une série chronologique suppose que le processus sous-jacent qui a généré les observations est un processus ARIMA. Cela peut sembler évident, mais contribue à justifier la nécessité de confirmer les hypothèses du modèle dans les observations brutes et dans les erreurs résiduelles des prévisions du modèle.
Un des problèmes majeurs avec une ARIMA est qu’elle ne prend pas en charge la saisonnalité – c’est à dire un cycle de répétition. La moyenne mobile intégrée saisonnière autorégressive, SARIMA, est une extension d’ARIMA qui prend explicitement en charge la composante saisonnière. La saisonnalité est traitée elle-même comme une ARIMA, avec des termes similaires aux composants non saisonniers du modèle. Toutefois elle implique de se baser sur des lags équivalent à la périodicité de la saison.
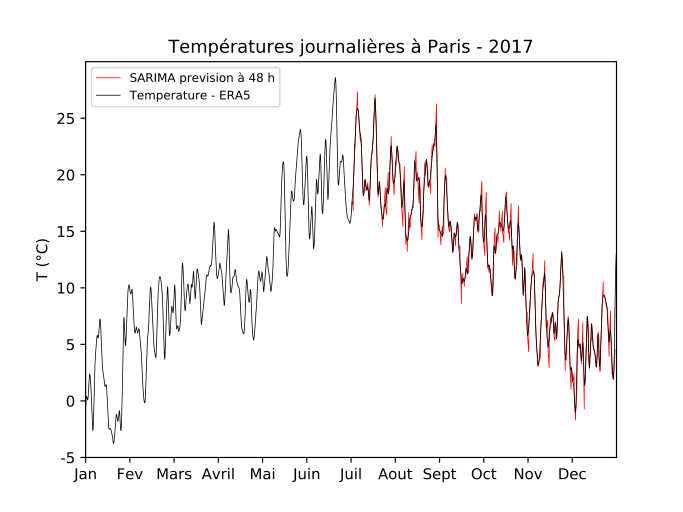
Illustrons cette fois la méthode SARIMA avec les températures parisiennes en 2017. A la figure 3, les prévisions à 48 heures de température avec une SARIMA calibré sur la première partie de l’année sont représenté en rouge.
Conclusion
La prévision des séries chronologiques peut s’avérer complexe et compliquée, mais de nombreuses techniques simples et efficaces, telles que le modèle ARIMA ou de Holt-Winters, peuvent offrir l’avantage de bon résultats pour un faible coût en efforts et complexité.
D’autres techniques plus complexes peuvent être utiles dans des cas très spécifiques, mais entraînent :
- Une perte de généralité qui nécessite une sélection pertinente des paramètres, avec de plus amples ajustements, suivant une expertise et des critères métiers (approche GLM/GAM).
Le modèle linéaire généralisé (GLM) est une généralisation de la régression linéaire. Le modèle additif généralisé (GAM) fusionne les propriétés du GLM avec celle du modèle additif. Ainsi, il devient facile de composer avec la saisonnalité de plusieurs périodes et de laisser l’analyste explorer des hypothèses sur les différentes composantes de la série chronologiques.
- Une perte en interprétabilité qui risque d’éroder la confiance des utilisateurs et complexifie le maintien en condition opérationnelle du modèle (approche deep learning). Les réseaux de neurones sont particulièrement utiles pour traiter de processus non linéaires. Ils fournissent parfois de premiers résultats satisfaisants sans même avoir besoin d’une vision précise de la structure et des propriétés de la donnée. Toutefois la construction de ce type de modèle peut rapidement s’avérer complexe tant les possibilités d’architecture sont nombreuses : RBM, HMM, DBN, CNN, RNN et combinatoire (CNN-RNN) !
par Marc Stefanon
Bibliographie
Holt, C. E. (1957). Forecasting seasonals and trends by exponentially weighted averages (O.N.R. Memorandum No. 52). Carnegie Institute of Technology, Pittsburgh USA.
Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: principles and practice. OTexts.
Winters, P. R. (1960). Forecasting sales by exponentially weighted moving averages. Management Science, 6, 324–342. https://doi.org/10.1287/mnsc.6.3.324